Capacitor Formulas

key equations and calculations for capacitors and capacitance in electronics circuits including charge, value, . . .

Capacitance Tutorial Includes:
Capacitance Capacitor formulas Capacitive reactance Parallel & series capacitors Dielectric constant & relative permittivity Dissipation factor, loss tangent, ESR Capacitor conversion chart

There are many calculations and equations associated with capacitors. The capacitor reactance equations and calculations are common, but there are many more capacitor calculations that may need to be performed.

Capacitor equations and capacitor calculations include many aspects of capacitor operation including the capacitor charge, capacitor voltage capacitor reactance calculations and many more.

Fundamental capacitor equations formulas and calculations

The fundamental capacitor equations or formulas and calculations are very useful in a number of areas of electronic circuit design. Although they may appear to be useful only for theoretical and academic situations, these equations and calculations can be very useful in practical scenarios as well.

Understanding the level of charge stored, the voltages present and the like are all particularly useful.

Basic capacitance formulae

The very basic capacitor equations link the capacitance with the charge held on the capacitor, and the voltage across the plates.

Capacitance is defined as the ability of an electrical or electronic component or circuit to collect and store energy in the form of an electrical charge. It is the amount of electric charge stored on a conductor for a stated difference in electric potential.

From this it is possible to define the basic equation for capacitance:

C = \frac{Q}{V}

Where
C is the capacitance in Farads
Q is the charge held on the plates in coulombs
V is the potential difference across the plates in volts

It is useful to be able to remember the basic equation for capacitance. It is used in a number of electrical and electronic circuit design applications.

To do this, it is helpful to use a memory triangle similar to that of the Ohm's law triangle, but using the capacitance variables instead.

C=Q/V the equation defining capacitance - triangle memory guide for the capacitance formula

It is very simple to use the capacitance calculation triangle. Simply cover up the unknown quantity and then and then calculate it from the other two. If they are in line they are multiplied, but if one is on top of the other then they should be divided.

For example if Q is required from a knowledge of C and V, then, because C and V are at the bottom of the triangle, and they are next to each other, then we can see that Q = C x V.< etc.

The summary above gives all the variations of the formula so that they can be remembered very easily.

Calculation of capacitance or parallel plate capacitor

One of the important basic calculations associated with capacitance is to be able to calculate the capacitance of a parallel plate capacitor.

Using the relevant formulas it is possible to accurately predict the capacitance of a capacitor from a knowledge of the area of the plates, the separation between them and the relative permittivity or dielectric constant of the material between the two plates.

Using this equation and basic theory, it is also possible to understand the stray capacitance levels on printed circuit boards and other aspects of electronic circuit design.

With speeds on electronic circuits becoming increasing fast as the technology for integrated circuits and the like improves, the levels of stray capacitance of the tracks, etc becomes increasingly important, and it can significantly affect the operation of the circuit. Accordingly it is necessary to take this into account for many circuit designs.

It is possible to deduce the capacitance of a capacitor from the equation below. The plates must be of the same size.

Capacitor definitions for the equation to determine capacitance of plate capacitor electronic component

C = ε_{r} ε_{0} \frac{A}{d}

Where:
C = capacitance in Farads
ε_r = relative permittivity for that medium
ε₀ = permittivity of space and it is equal to 8.854x10^-12 F/m
A = the area of one plate in square metres
d = distance between the two plates in metres

Determining the capacitance for a plate capacitor is very useful for where ordinary flat capacitors are to be used. However it is sometimes necessary to be able to determine the capacitance for a tubular capacitor. One example of this is when it is necessary to determine the capacitance of a length of coaxial feeder.

Capacitor definitions for the equation to determine capacitance of tubular capacitor electronic component

This can easily be accomplished using a slightly modified version of the formula for the plate capacitor which has been adapted to accommodate the different geometry of the tubular capacitor.

C = \frac{2 π ε_{r} ε_{0} l}{\log (\frac{a}{b})}

These are the most widely used instances where it is necessary to calculate the capacitance of an item. It is possible to derive the relevant formulas for other geometries, but they tend to be more individual and not widely used.

The dielectric constant and relative permittivity are used within these equations. Gain a greater understanding . . .

Read more about . . . . Permittivity, relative permittivity & Dielectric Constant.

Energy stored in a capacitor

Another important equation associated with capacitors is to determine the amount of energy stored in the capacitor.

The energy stored in the capacitor is equal tot he work that was required to pace the charge into the capacitor.

If the voltage at any instant is "v", and a small amount of charge δq is transferred at this voltage, then the work done will be v δq.

Hence the total work done, and accordingly the energy stored in the capacitor is:

W = \int_{0}^{Q} V d Q

From this we can see:

W = \int_{0}^{Q} \frac{q}{C} d Q

Accordingly:

W = \frac{1}{2} C V^{2}

These equations and formulas are very useful in many areas of electronic circuit design to determining the level of charge in a capacitor. This can be very important in many situations including power supply design, determining the capacity required for capacitors used for hold up situations where the power may be interrupted and many other situations.

Capacitance infographic

I've put together a useful infographic detailing the key equations and concepts of capacitance. It provides some of the more useful equations as well as details about the concepts, etc.

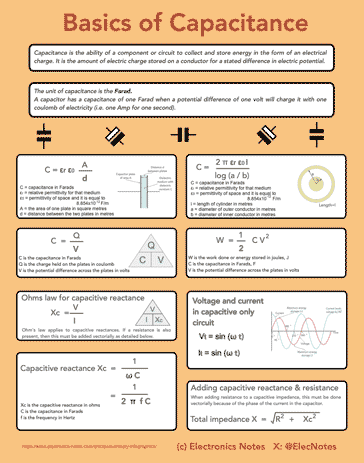
Capacitance basics infographic
*Click on image for larger version*

The basic equations for capacitors and their capacitance enable the levels of capacitance to be calculated, along with the energy stored within them. These are some of the key basic formulas and attributes needed for basic capacitor theory.