Capacitive Reactance: what it is, calculations & calculator

The capacitive reactance is a measure of how a capacitor restricts the flow of alternating current, although similar to resistance, it is not the same.

Capacitance Tutorial Includes:
Capacitance Capacitor formulas Capacitive reactance Parallel & series capacitors Dielectric constant & relative permittivity Dissipation factor, loss tangent, ESR Capacitor conversion chart

We are familiar with the way resistors restrict the flow of electrical charge because of their resistance and Ohm's Law, but capacitors can also impede the flow of electrical charge with an alternating current as a result of their reactance.

It is important to know what effect a capacitor will have on any circuit in which it operates. Not only does it prevent the direct current component of a signal from passing through, but also has an effect on any alternating signal that may appear.

Being able to calculate the level of reactance is important because capacitors are used in many electrical and electronic circuit designs. Also knowing how this reactance affects the current flow with other electronic components is also of great importance.

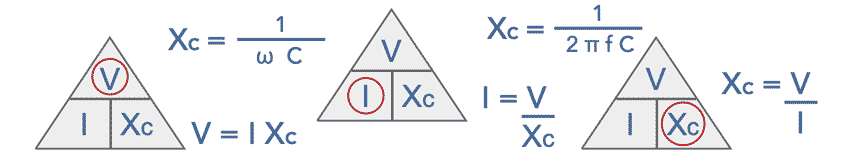
Header showing the various capacitive reactance calculations and formulas

What is capacitive reactance

In a direct current circuit where there may be a battery and a resistor, it is the resistor that resists the flow of current in the circuit. This is basic Ohms Law. The same is true for an alternating current circuit with a capacitor.

A capacitor with a small plate area will only be able to store a small amount of charge, and this will impede the flow of current. A larger capacitor will allow a greater flow of current.

In view of the differing levels of charge storage, it can be seen that if only a small level of charge can be stored, this will present a greater level of restriction on the current that can be passed by the capacitor than one that can store much more charge.

The 'restriction' on the current that can be passed by a capacitor is called the reactance of the capacitor.

The reactance of a capacitor is different to the resistance of a resistor, but it is nevertheless measured in Ohms just the same. The reactance of a capacitor is dependent upon the value of the capacitor and also the frequency of operation. The higher the frequency the smaller the reactance.

It is found that the greater the frequency the lower the reactance and a curve such as that shown below is seen for a capacitor of a given value.

Capacitive reactance vs frequency showing how the reactance falls with increasing frequency - reactance is inversely proportional to frequency — Capacitive reactance vs frequency

Calculating the reactance of a capacitor

It can be imagined that the larger the capacitor, the more charge it can store and hence the less it will restrict current flow.

Also the frequency by which the current alternates has a major impact. If the frequency is higher, it means that there is a greater change in the stored charge and hence the restriction on current, i.e. reactance is less.

The basic equation for the reactance of a capacitor is:

X_{c} = \frac{1}{ω C}

Where
X_c is the capacitive reactance in Ohms
ω is the angular velocity in radians per second
C is the capacitance in Farads

However it is normally far more useful to calculate the reactance with a knowledge of the frequency. Frequency in cycles per second or Hertz is far more widely used as a unit than the angular velocity.

X_{c} = \frac{1}{2 π f C}

Where
X_c is the capacitive reactance in Ohms
f is the frequency in Hertz
C is the capacitance in Farads

As an example it is possible to calculate the reactance of a capacitor with a capacitance of 1 µF at a frequency of 1kHz.

Substituting directly into the equation, and using 2 π as 6 which is a sufficiently close approximation for most calculations.

X_{c} = \frac{1}{2 π 10^{3} 10^{- 6}}

This simplifies down to give:

X_{c} = 166 Ω

In this way it can be seen that it is very easy to calculate the reactance of a capacitor. The main point to watch is that all the frequencies and capacitances are measured in Hz and Farads. Keeping track of the zeros or power of ten multipliers in the figures is key to obtaining the right answer.

Capacitor Reactance Calculator

Enter the capacitance value (in Farads) and frequency (in Hz) to calculate the capacitive reactance (Xc) of the capacitor.

Capacitance (C)	Frequency (f)	Reactance (Xc)
Capacitor Reactance Calculator

Current calculations

The next stage is to look at how the current, for example can be calculated for a capacitor such as the one above.

If the only component present is the capacitor, then it is simply a matter of applying Ohm's law and calculating the voltage or current, etc from a knowledge of the other two variables. It is also possible to calculate the reactance from a knowledge of the voltage and current.

V = I X_{c}

It is simply a matter of replacing 'R' in the Ohm's Law equation with X_c.

It is also possible to use the Ohm's law triangles to calculate the values of unknown variable.

The Ohm's law triangle expressed for capacitive reactance

It can be seen that the resistance R normally seen int he Ohm's Law equation and the Ohm's law triangle has simply been replaced by the capacitive reactance X_c.

Adding resistance and reactance

Although resistance and reactance are very similar, and the values of both are measured in Ohms, they are not exactly the same. The current and voltage are 90° out of phase and whereas for a resistor they are in phase.

As a result it is not possible to add the resistor resistance and the capacitor reactance directly together.

Instead they have to be summed "vectorially". In other words it is necessary to square each value, and then add these together and take the square root of this figure. Put in a more mathematical format:

Z_{total}^{2} = X_{c}^{2} + R^{2}

This can be expressed more conveniently for calculations as:

Z_{total} = \sqrt{X_{c}^{2} + R^{2}}

By adding the two quantities in this way it is possible to calculate the overall impedance for the combination of resistor and capacitor.

It is also possible to use Ohm's law to calculate the current and voltage, etc in the normal way.

Capacitive reactance is a key quantity in all forms of electrical electronic circuit. As capacitors are used in virtually all electronic products, understanding how to calculate the reactance and how this interacts with resistors and other electronic components is a key element for many electronic circuit designs. Even though the calculations are relatively straightforward, they are very important in many areas.