Parallel & Series Resistors: formulas; calculator, etc

Formulas, calculations and a calculator for determining the overall resistance of resistors placed in series and parallel.

Resistance Tutorial Includes:
What is resistance Ohms Law Ohmic & Non-Ohmic conductors Resistance of filament lamp Resistivity Resistivity table for common materials Resistance temperature coefficient Voltage coefficient of resistance, VCR Electrical conductivity Series & parallel resistors Parallel resistors table

Resistors can be placed in many configurations in an electrical or electronic circuit - sometimes in series, at other times in parallel.

When they are placed in these configurations it is important to be able to calculate the overall resistance. This can be achieved quite easily when the right formulas are used - there are simple formulas for both series and parallel resistors.

Electronic component resistors in series and parallel circuit configurations

As electronic circuit design is undertaken, or whether it is for another reason, being able to calculate the resistance of combinations of resistors can be very useful.

In electronic circuits, combinations of resistors can be reduced to series elements and parallel elements, although when other electronic components are used the combinations can be more complicated. However in many instances calculating the series and parallel resistance values is of great importance.

Video: How to calculate Resistors in Series & Parallel

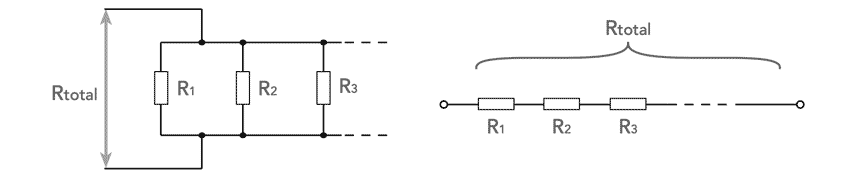
Resistors in series

The simplest electronic circuit configuration is that of resistors being placed in series. This can occur if a number of these electronic components are placed in series, or whether the resistance of a cable needs to be added to that of a resistor, etc.

If the resistors are placed in series then the overall resistance is simply the sum of the individual resistors.

The value of the resistors or resistances placed in series can be expressed mathematically as follows:

Rtotal = R 1 + R 2 + R 3 + . . . . . .

Read more about . . . . derivation of formula for resistors in series.

Example of calculating resistors in series:
As an example, if three resistors having values of 1kΩ, 2kΩ and 3kΩ are placed in series then the total resistance is 1 + 2 + 3 kΩ = 6kΩ.

In real life situations and aspects of electrical and electronic circuit design there will be many areas where there are electronic components such as resistors, or other items introducing resistance where a number of resistances in series which need to be summed.

Resistors in parallel

There are also many instances where electronic components such resistors as well as other items introducing resistance appear in an electrical or electronic circuit in parallel.

If resistors are placed in parallel they share the current and the situation is a little more difficult to calculate, but still quite easy.

\frac{1}{Rtotal} = \frac{1}{R1} + \frac{1}{R2} + \frac{1}{R3} + . . . . . .

Read more about . . . . derivation of formula for resistors in parallel.

Example of calculating resistance of resistors in parallel:

To give an example if there are three resistors in parallel with values of 100Ω, 50Ω and 20Ω then the overall value of the combination can be worked out:

The first stage is to take the basic equation and then substitute the values into it.

\frac{1}{R_{t}} = \frac{1}{R_{1}} + \frac{1}{R_{2}} + \frac{1}{R_{3}} + ... . .

With resistors of 100Ω 50Ω and 20Ω in parallel, this becomes:

\frac{1}{R_{t}} = \frac{1}{100} + \frac{1}{50} + \frac{1}{20}

\frac{1}{R_{t}} = 0.01 + 0.02 + 0.05

\frac{1}{R_{t}} = 0.08

Multiply both sides by R_total - as the same operation has been done to both sides it keeps the equation balanced.

1 = 0.08 \cdot R_{t}

Now divide both sides by 0.08.

R_{t} = \frac{1}{0.08} = 12.5 Ω

Case of only two resistors in parallel

In many electronic circuit designs the most common instance of resistors in parallel consists of only two electronic components.

It is often the case that one resistor is placed in parallel with another. Or another instance may be where a resistor is placed across the terminals for a circuit or network that has a certain resistance. In this case, it is only necessary to calculate the overall resistance for two resistors in parallel.

Where it is necessary to calculate the overall value for two resistors parallel, the equation can be manipulated and considerably simplified as shown below:

R_{total} = \frac{R_{1} R_{2}}{R_{1} + R_{2}}

This formula considerably simplifies the calculation of the value of two resistors in parallel as it only requires one multiplication, one addition and one division to be done. This can often be achieved mentally or on a scrap of paper. Alternatively our simple calculator for two resistors in parallel given below can be used.

Calculator for two resistors in parallel

This parallel resistance calculator provides an easy method for calculating the overall resistance for two resistors connected in parallel.

Although a parallel resistor value calculation for two resistors simplifies to a simple formula, sometimes it is much easer and faster to be able to use a calculator.

To use the parallel resistors calculator, just enter the values of the parallel resistors in ohms, Ω or kΩ, etc in the two input boxes, but note all values must be in the same units, i.e. both on Ω kΩ MΩ etc.. The parallel resistor calculator will then provide the overall resistance of the two resistors in the same units as the input.

Enter the two values for the resistors, R1 and R2 in the boxes provided in the calculator below, press calculate and the total resistance will be provided.

Parallel Resistance Calculator

The parallel resistors calculator provides an easy way to calculate the resistance of two resistors in parallel saving writing everything down and resorting to pen and paper or a calculator of some form.

Knowing how to calculate the values for resistors in series and parallel is key to understanding the way in which electrical and electronic circuits work. These concepts are used as second nature in electrical and electronic circuit design.