Electrical Resistivity; definition, formula & units
Electrical resistivity is a key parameter for any material used in electrical circuits, electronic components and many other items.
Resistance Tutorial Includes:
What is resistance
Ohms Law
Ohmic & Non-Ohmic conductors
Resistance of filament lamp
Resistivity
Resistivity table for common materials
Resistance temperature coefficient
Voltage coefficient of resistance, VCR
Electrical conductivity
Series & parallel resistors
Parallel resistors table
Resistivity is a measure of the resistance of a given size of a specific material to electrical conduction and it is an important parameter for all substances associated with electrical usage, electronic circuit design, etc.
Resistivity may also be referred to as the specific electrical resistance, or volume resistivity, although these terms are less widely used.

Although materials resist the flow of electrical current, some are better at conducting it than others.The resistivity is a figure that enables comparisons of the way in which different materials allow or resist current flow.
To enable resistivity figures to be meaningful, specific units are used for resistivity, and there are formulas for calculating it and relating it to the resistance in Ohms for a given size of material.
Materials that conduct electrical current easily are called conductors and have a low resistivity. Those that do not conduct electricity easily are called insulators and these materials have a high resistivity.
The resistivity of different materials plays a major role in selecting the materials used for electrical wire, within many electronic components including resistors, integrated circuits and many more.
The resistivity of a material will also help categorise whether a material is a conductor, insulator or a semiconductor, and as a result this helps with understanding the best uses or applications for them.
Resistivity definition & units
The electrical resistivity of a specimen of a material may also be known as its specific electrical resistance. It is a measure of how strongly a material opposes the flow of electric current.
In order to understand what resistivity is a little more precisely, it often helps to have a definition of what it is. Although this may be a little formal in some respects, a concise definition can often help give a more exact understanding of what it is.
Resistivity definition:
The resistivity of a substance is the resistance of a cube of that substance having edges of unit length, with the understanding that the current flows normal to opposite faces and is distributed uniformly over them.
The electrical resistivity is the electrical resistance per unit length and per unit of cross-sectional area at a specified temperature.

The SI unit of electrical resistivity is the ohm⋅metre (Ω⋅m). It is commonly represented by the Greek letter ρ, rho.
Although the SI resistivity unit, the ohms metre is generally used, sometimes figures will be seen described in terms of ohm centimetres, Ω⋅cm.
As an example, if a solid cube of material with dimensions of 1 M3 has sheet contacts on two opposite faces which do not introduce any resistance themselves, and the resistance between the contacts is 1 Ω, then the resistivity of the material is said to be 1 Ω ˙⋅m.
To re-iterate it, this means that the resistivity is measured for cube of the material measuring a metre in each direction.
Resistivity formula / equation
The resistivity of a material is defined in terms of the magnitude of the electric field across it that gives a certain current density. It is possible to devise an electrical resistivity formula.
Where:
ρ is the resistivity of the material in ohm metres, Ω⋅m
E is the magnitude of the electric field in volts per metre, V⋅m^-1
J is the magnitude of the current density in amperes per square metre, A⋅m^-2
Many resistors and conductors have a uniform cross section with a uniform flow of electric current. It is therefore possible to create the more specific, but more widely used electrical resistivity formula or equation:
Where:
R is the electrical resistance of a uniform specimen of the material measured in ohms
l is the length of the piece of material measured in metres, m
A is the cross-sectional area of the specimen measured in square metres, m^2
It can be seen from the equations that the resistance can be varied by changing a variety of different parameters.
For example, keeping the material resistivity constant, the resistance of the sample can be increased by increasing the length, or decreasing the cross sectional area. It can also be seen from the resistivity equations that increasing the resistivity of the material will increase the resistance assuming the same dimensions. Similarly decreasing the resistivity will decrease the resistance.
Material resistivity levels
Materials are put into different categories according to their level or resistivity. A summary is given in the table below.
| Resistivity Regions for Different Categories of Materials | ||
|---|---|---|
| Material type | Resistivity region | |
| Electrolytes | Variable* |
|
| Insulators | ~10^16 |
|
| Metals | ~10^-8 |
|
| Semiconductors | Variable* |
|
| Superconductors | 0 |
|
* The level of conductivity of semiconductors is dependent upon the level of doping. With no doping they appear almost like an insulator, but with doping charge carriers are available and the resistivity falls dramatically. Similarly for electrolytes, the level of resistivity varies widely.
The definition of resistivity states that the resistivity of a substance is the resistance of a cube of that substance having edges of unit length, with the understanding that the current flows normal to opposite faces and is distributed uniformly over them.

Practical implications of resistivity
The resistivity of materials is important as it enables the right materials to be used in the right places in electrical and electronic components.
Materials used as conductors, for example in electrical and general connecting wire need to be able to have a low level of resistivity. This means that for a given cross sectional area, the resistance of the wire will be low. Selecting the right material depends on knowing its properties, one of which is its resistivity.
As an example, copper is a good conductor as it provides a low level of resistivity, its cost is not too high, and it also provides other physical characteristics that are useful in many electrical and electronic applications. The resistivity of copper is around 1.7 x 10-8 ohm metre (or 17. nΩm), although figures will vary slightly according to the grade of the copper
Materials like copper and even aluminium provide low levels of resistivity and this makes them ideal for use as electrical wires and cables - copper often being the favourite. Silver and gold have much low resistivity values, but as they are considerably more expensive, they are not widely used. However, silver is sometimes used to plate wires where its low resistivity is essential, and gold flashing is used for the mating surfaces of many electronic connectors to ensure the best contacts. Gold is also good for electrical connectors as it does not tarnish or oxidise like other metals.

Other materials are required to act as insulators, carrying as little current as possible. The resistivity of an insulator will be many orders of magnitude higher. One example is air and this has a very resistivity figure of over 1.5 x 1014, which can be seen to be very, very much higher than the resistivity of copper.
Electrical resistivity is important in many other electronic components. In resistors for example the resistivity of various materials is key in making resistors have the right resistance.
Resistivity is also key in other electronic components as well. For integrated circuits the resistivity of the materials in the chip is very important. Some areas need to have a very low resistance and able to connect different areas of the IC internally, whereas other materials need to isolate different areas. Again, the resistivity is important to make this happen.
Resistivity is key in many areas of electronic components as well as for many electrical parts as well.
Resistivity infographic
To provide a handy reference, I've put together a useful infographic about resistivity, the major equations and some of the resistivity figures for more commonly used materials.
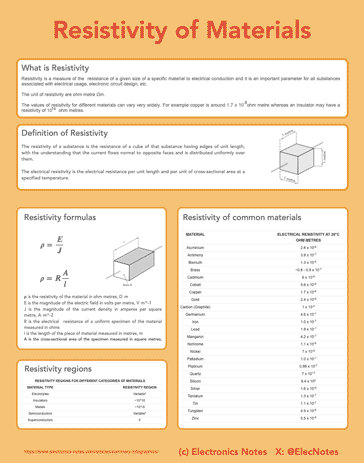
Click on image for larger version
Electrical resistivity is a key parameter for material that are to be used with electrical and electronic systems. Those substances with a high electrical resistivity are termed insulators and can be used for this purpose. This with a low level of electrical resistivity are good conductors and can be used in a host of applications from wire, to electrical connections and much more.
 Written by Ian Poole .
Written by Ian Poole .
Experienced electronics engineer and author.
More Basic Electronics Concepts & Tutorials:
Voltage
Current
Power
Resistance
Capacitance
Inductance
Transformers
Decibel, dB
Kirchoff's Laws
Q, quality factor
RF noise
Waveforms
Return to Basic Electronics Concepts menu . . .



