What is a Constant-K Filter: the basics

The constant k filter is one of the most straightforward to design, using very simple equations - although the performance is not as good as some other types, its performance is adequate for many applications.

Home » Radio & RF technology » this page

Constant K Filter Includes:
Constant-k filter Simple LC LPF design LC HPF design LC band pass filter design

Filter basics includes:: RF filters - the basics Filter specifications RF filter design basics High & low pass filter design Constant-k filter Butterworth filter Chebychev filter Bessel filter Elliptical filter

Constant k filters are a form of filter that is designed using what is termed an image method. The constant k filters are the original and simplest filters produced by this methodology and consist of a ladder network of identical sections of passive components.

The constant k filters were the first filters that could approach an ideal filter for of response.

Although not widely used today as a result of the fact that their response is inferior to other forms of filter, they do have the advantage that the design equations can be particularly easy to calculate, and this means that they can be used by many who do not have filter design experience.

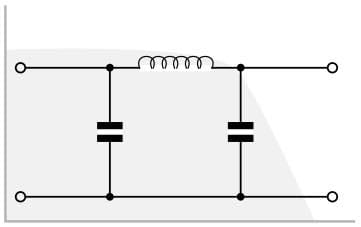
Constant k filter basics

The building block of constant k filters is the half-section "L" network, composed of a series impedance Z, and a shunt admittance Y. The constant k filter gains its name from the mathematical relationship between the series and shunt impedances.

k^{2} = \frac{Z}{Y}

It can be seen that K is constant for the filter.

Constant K filter advantages and disadvantages

Like any approach taken within electronic design, there are advantages and disadvantages. This is naturally true for constant-k filters. These points need to be taken into account when undertaking the design and it may be necessary to mitigate against some of the effects if they are used.

Constant K filter advantages:

Constant k filters are easy to design - simple equations can normally be employed.
The filter attenuation in the stop band tends to infinity at frequencies that are distant from the cut-off frequency.

Constant K filter disadvantages:

The filter attenuation increases very slowly and this means that the pass-band and stop-band are not always well defined.
There are significant impedance variations with frequency even within the pass-band. If impedance matching is required, then this can be an issue and may need to be overcome - possibly with the use of attenuators, although this reduces the signal level.

Constant k filter designs

It is possible to realise simple circuit designs for the constant k filter for low pass, high pass and band pass filters:

Low pass filter : Like all low pass filters, the constant k low pass filter enables lower frequencies to pass relatively un-attenuated, whilst rejecting higher frequency signals, i.e. those above the cut-off frequency.
Read more about . . . . Low Pass Constant K Filter.
High pass filter: Like all high pass filters, the constant k high pass filter enables those frequencies above the cut-off frequency to pass with little attenuation, whilst those below the cut-off are removed.
Read more about . . . . High Pass Constant K Filter.
Band pass filter: The band-pass constant k filter has a band of frequencies it allows through the filter. Other frequencies are attenuated.
Read more about . . . . Band Pass Constant K Filter.

The constant k filter can be used in a number of areas where a simple to calculate filter is required. Although the performance will not be as good as other forms of filter that are now in common use, the simplicity of calculation makes the constant k filter an attractive proposition in some instances.