RF filter design basics

RF filter design follows some key methodologies to enable the calculations to be made in the most effective way.

Home » Radio & RF technology » this page

RF Filters Includes:
RF filters - the basics Filter specifications RF filter design basics High & low pass filter design Constant-k filter Butterworth filter Chebychev filter Bessel filter Elliptical filter Crystal filter

RF filter design is often thought to be difficult and reserved only for specialist developers. Although RF filter design can be complicated, the process can be simplified and opened out to enable it to be accomplished by and electronic designer.

To ensure that the optimum design is achieved for the RF filter, it is necessary to have the required performance parameter requirements in place so that decisions can be made about topology, filter types and the like.

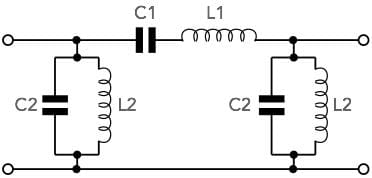
An example of a typical LC bandpass filter

However, whatever the actual filter design needed, the same basic methodology is used to design any filter. Using a methodology means that all the necessary requirements are taken on board, the right design approach used, and ultimately the correct RF filter is designed.

RF filter design basics

In general terms, filters modify the amplitudes and phases of sinusoidal waveforms that pass through them. This change varies according to the frequency of the individual sinusoids within the overall waveform.

Most filters are what is termed linear filters. As such they have no non-linear actions in which the response is proportional to the input. Instead the signals pass through and their amplitude and phase is altered in a linear fashion according to their frequency.

From this it is possible to determine some of the key RF filter design parameters which are the factors by which the signal is changed, namely the gain, G and the phase shift θ. As both the gain G and the phase shift θ are dependent upon the frequency, i.e. they are functions of frequency, they can be expressed as follows:

G = G (f)

θ = θ (f)

These two functions represent the magnitude response (often referred to as the frequency response) and the phase response of the filter respectively.

These two functions govern the major features that need to be known about the filter. In being able to determine the functions it is possible to design the RF filter.

Normally the example of the low pass RF filter design is used in the first instance and then this is expanded to include other forms of filter. Accordingly we will look at low pass filter design first.

Real and ideal filters

When designing an RF filter it would be ideal if the filter would allow signals within the pass-band through without any change in amplitude or phase. Filters like this could have a rectangular response, falling straight to their stop-band and giving the required level of stop-band attenuation.

Unfortunately it is not possible to design RF filters like this, and real RF filter designs can only approximate to the ideal response curves and parameters. These approximations can then be used as the different types of filter that exist. These include the Butterworth, Bessel, Chebyshev, Elliptical, Gaussian and many more.

Using a mathematical approach for RF filter design, it is possible to use a mathematical relationship. It can be proved that the square of the response for all realisable filters can be expressed as the ratio of two even, i.e. rational polynomials. This means that a generic mathematical expression for all RF filter designs is:

G^{2} f = \frac{B^{2} (f)}{A^{2} (f)}

RF filter design & normalisation

While relatively straightforward equations are available for Butterworth filters and constant-K filters, other forms of filter require more complicated calculations.

The approach to RF filter design that has been used for many years uses what are termed normalised filters. A set of variables is calculated for a standard set of conditions and these and tabulated ready for use and scaling to the required conditions.

A normalised filter would have a cut-off frequency of 1 radian per second, i.e. 0.159Hz and an impedance of 1Ω. These values can then be scaled very easily for use at the required frequency and impedance. In this way the tedious and involved mathematics required for RF filter design was reduced to little more than determining the requirements and then finding the relevant table of values. The tables are available in a variety of books and even on-line.

The requirements that first need to be chosen include parameters such as the filter type (Butterworth, Chebyshev, etc.), level of ripple, etc, filter order (i.e. the number of inductors and capacitors), etc.

Once these are chosen the relevant table can be found and the values for the elements in the filter determined.

RF filter design & scaling

Once the filter design has been realised in its normalised form, it is then necessary to transform the values to the required frequency and impedance. In the normalised format the filter design has a cut-off of 0.159 Hz, i.e. 1 radian per second and it is designed to work into a load resistance of 1 Ω.

C = \frac{C_{n}}{2 π f_{c} R}

L = \frac{R L_{n}}{2 π f_{c}}

Where:
C = real capacitor value
L = real inductor value
Cn = normalised capacitor value
Ln= normalised inductor value
R = required load resistor value
fc = required cut-off frequency

RF filter design process

There are a number of steps or stages in the RF filter design process. Following these in order helps the RF filter to be designed in a logical fashion. These steps are for the low pass filter design - further stages for transferring this to a high pass or band pass filter are given on the following pages.

While some computer programmes may allow direct design, often design using tables, etc. is still widely used. If a computer programme is used, the filter design process can be modified accordingly.

Define response needed: the first stage in the process is to actually define the response required. Elements such as cut-off point, attenuation at a given point, etc..
Normalise frequencies: In order to be able to use the various tables and diagrams of filter curves, it is necessary to convert all frequencies so that the cut-off point is at 1 radio per second and any other points are relative to this.
Determine maximum pass-band ripple: One of the major steps in the RF filter design is to understand how much in-band ripple can be tolerated. The more ripple, the greater the level of selectivity that can be obtained. The greater the selectivity the faster the transition from pass-band to ultimate roll off will be .
Match required attenuation curves with those from filter: With a knowledge of the characteristics, both in terms of ripple and rejection required at particular points, it is possible to determine the filter type and also the order or number of elements required within the filter design.
Determine element values: Using the relevant look up tables the normalised filter component values can be determined
Scale normalised values: Finally the values need to be scaled for the required cut-off frequency and resistance.

Filter values and curves can be found in a number of filter design books including "Handbook of Filter Synthesis" by Zvrev, pub Wiley.

Today many circuit design and filter design programmes or Apps are available on-line or as an application download.

Using these applications, it is often possible to feed in the requirements directly and for the design to appear. However it is still advisable to be able to understand the design process from basic principles and in this way the trade-offs limitations can be better understood.

Understanding the basics of RF filter design not only enables filters to be designed, but even if the actual design is not undertaken, it provides a greater insight into the process and the specification of the filters themselves.