What is a Sine Wave - Electronics Waveform

Electronic & Electrical Waveforms Includes:
Waveform types & basics     Sine wave     Square & rectangular waves     Triangular wave    

Sine waves are one of the most common forms of electrical or electronic waveform. Sine waves are the waveform that is seen when displaying electrical supply or mains waveforms, most RF or radio frequency waveforms, as well as some audio test signals.

Sine waves are also found in many other areas of science and life in general because huge numbers of mechanical and other items vibrate - clock pendulums are but one of very many examples.

The sine wave is the most basic of signals, and when undistorted it does not contain any harmonics - just the single frequency of the signal, unlike other waveforms that contain harmonics.

Sine waves (and not sign waves as has been seen in some cases) are electronic waveforms that oscillate smoothly either side of a central value - normally zero volts, although they can oscillate about another voltage.

Sine wave basics

The sine wave follows a sine curve alternating equally either side of a central value. If the sine wave is displayed on an oscilloscope screen, it can be seen that there are several parameters that can be measured and used.

The sine wave follows the values of sine over the period of the cycle. As one cycle is equivalent to 360° or 2Π radians, the instantaneous value of sine can be calculated from the angle in degrees or radians, i.e. how far advanced the waveform is in its cycle.

Parameters like the phase angle, amplitude, time period and the like can all be seen.

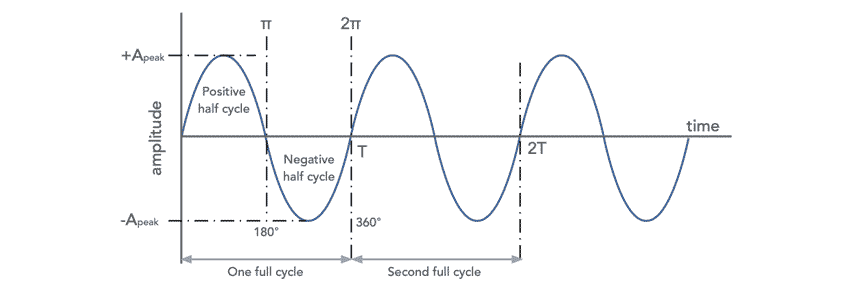
The diagram below shows some of the main parameters of interest for the sine waveform including the time period, phase, amplitude and the like.

It is worth looking at the different parameters separately and explaining more about them in turn.

• Amplitude:   It can be seen that the amplitude varies across the cycle, but two points which can easily be measured are the positive peak identified as +A_peak and the negative peak identified as -A_peak.

  Often the peak voltage of a sine wave is used as this is the voltage that would be generated if the waveform was fed into a diode rectifier with a smoothing capacitor after it. The capacitor would charge up to the peak voltage and hold this value, assuming there is no load.

  Another value known as the peak to peak voltage may also be used in some instances and this is just the total voltage between +A_peak and -A_peak, i.e. it is twice +A_peak.

• Time period:   the time period is the period of time between one point on one cycle of the waveform and the corresponding point on the next one. In other words, it is the time for one complete cycle.

  Normally the most convenient point to take on a sine wave centred about 0V is the place where it crosses the 0V line. It is very easy for logic, or other circuitry to detect the zero crossing point for the positive (or negative) going edge.

• Phase:   The phase of a sine wave can be understood as the horizontal position of a waveform with respect to one cycle. Looking at the diagram below, it can be seen that the instantaneous phase of the waveform with respect to the start is the angle that is angle that is between the start of the waveform and the current position.

  

  This is often depicted on a circle, the being the vertical height as shown.

  The phase can be measured in degrees or radians and can be assigned the variable θ, or ϕ

  it is often easier to have the concept of phase difference between two waveforms. Again using the concept of the circle, it is the angle between the positions of the two waveforms when depicted on a circle.

  

  When viewed as the phase difference between two sine waves when viewed, for example on an oscilloscope, it can be seen as the difference in the position of the two waveforms.

  

• Frequency:   Although not directly visible from a waveform like the one shown in the diagram above, the frequency of a sine wave is still very important.

What does a sine wave sound like

A sine wave sounds like a very smooth note. In fact the perfect sine wave has no distortion and as a result it consists of a single tone with no harmonics.

Musically a sine wave is not considered to be an interesting waveform - more interesting sounds typically are more complicated and rich in harmonics. In fact it is the harmonics that change the shape of the waveform, even if it is only a single tone.

Sine wave mathematics

The sine wave is called a sine wave because it follows the pattern of the geometric value of sine over the complete cycle.

Where:
    A = amplitude, the peak deviation of the function from zero.
    f = frequency, measured in cycles per second, i.e. Hertz, Hz.
    ω = the angular frequency, in radians per second, 2πf.
    ϕ = phase, specified (in radians) where in its cycle the oscillation is at t = 0.

Sine and Cosine Waves

In the same way that sine and cosine are linked within mathematics, so too, there are links and large similarities between sine and cosine waveforms.

Looking at the equation for a sine wave: A sin(ωt + ϕ), of the starting phase difference ϕ is made equal to 90° or π/2, then the sine wave will start at the positive peak and be equal to the cosine wave.

In other words the cosine wave is the sine wave delayed by a quarter of a cycle.

Effectively the cosine wave is an specific case of a sine wave which is delayed by the phase ϕ where ϕ is 90° or π / 2.

Sine wave spectrum

A sine wave is a special form of signal because a pure sine wave consists of a single frequency. An ideal sine wave has no harmonics or other frequencies.

Musically this might make it rather uninteresting, but for many electronic circuits it is the ideal signal.

Although a pure sine wave does not contain any harmonics and is a very simple waveform, using Fourier analysis it can be shown that other periodic waveforms can be made up from a series of sine waves.

For example a square wave is made up from a series sine waves of odd-integer harmonics of the required amplitude. Other waveforms can be similarly analysed and their constituent sine waves can be discovered.

The sine wave is one of the most important forms of periodic waveform. Using Fourier analysis it can be seen to form all other forms of periodic waveform and as such it is at the centre of all signals and signal processing.

The sine wave can be seen in many areas of science and everyday life as it forms the basis of many vibrating systems, and as in electronics, using Fourier analysis, these waveforms can be analysed as many sine waves acting together.

Although, musically it is not the most interesting of sounds, the sine wave is nevertheless a very important waveform in many areas of science.

More Basic Electronics Concepts & Tutorials:
Voltage     Current     Power     Resistance     Capacitance     Inductance     Transformers     Decibel, dB     Kirchoff's Laws     Q, quality factor     RF noise     Waveforms    
    Return to Basic Electronics Concepts menu . . .